تاريخ : شنبه 8 آذر 1393 | یازار : علی فتحی (آلتین)
+0 به یه ن
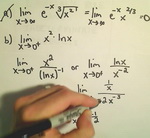
با روش رفع ابهام هوپیتال بیشتر آشنا شوید. |
|
|
تعاریف و مفاهیم ریاضی: قاعده هوپیتال |
|
گیوم دو لوپیتال (Guillaume de l'Hôpital) |
|
|
قاعده
هوپیتال یا لوپیتال (به فرانسوی: L'Hôpital) در حساب، روشی است كه با
استفاده از آن می‌توان حد تابع را، در صورت وجود، در نقطه‌ای كه مقدارآن 0/0 'صفر تقسیم بر صفر' یا ∞/∞ 'بینهایت تقسیم بر بینهایت' است بدست آورد.
گفته
می شود قاعده ای كه امروزه به نام هوپیتال (ریاضیدان فرانسوی قرن هفدهم)
شناخته می شود، در واقع از كشفیات یوهان برنولی می باشد. هوپیتال این قانون
را در سال 1696 در كتابی منتشر نمود و البته از همكاری برادران برنولی هم
قدردانی نموده است. در حالیكه نامه ای بدست آمده است كه در آن یوهان برنولی
قاعده مذكور را همراه با اثبات آن ارائه نموده بوده است.
تعریف ریاضی:
فرض كنید f و g توابعی باشند كه بر بازهٔ بازی چون I، بجز احتمالاً در عددی مانند c از I، مشتق پذیرند. در این صورت اگر
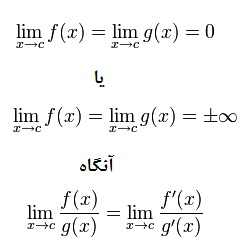 قاعده هوپیتال را می توان در موارد زیر نیز به كار برد:
1∞, 00, ∞0, 0 × ∞, ∞ − ∞
چند مثال از به كارگیری قاعده هوپیتال:
 |
|
|
|
گؤنده ر
بؤلوم لر:
تعاریف و مفاهیم ریاضی: قاعده هوپیتال
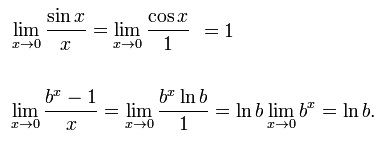یارپاق لار:
[1]